Comment ça marche ?

27 août 2019 Non Par u3padmin

Sans photons, pas de lumière, donc pas de vie… et, encore moins d’U3P. Car ce sont ces petits « grains de lumière » qui appliquent une force sur notre voile.

Voyons comment ça marche…

Vous savez que la lumière, qu’elle vienne du Soleil ou de votre lampe à pétrole, est un phénomène ondulatoire (une « vibration » d’énergie) dont la fréquence $\nu$ (prononcer « nu », le n en grec) est de l’ordre de $5 \times 10^{14}$ Hertz pour le visible – donc environ 500 milliards de fois plus rapide que la fréquence d’un son audible, et 3 milliards de fois plus que les émissions radios G.O. de France Inter, par exemple. On a montré que cette énergie n’était pas continue, mais était groupée en petits grains: les photons, d’énergie $E = h\times \nu$ (h étant la constante de Planck).

D’où la fiche d’identité du photon visible :

Forme : personne ne l’a vu ! on le dessinera comme ça :

En fait, c’est un paquet d’ondes.

Masse : nulle

Vitesse : celle de la lumière, $c = 3 \times 10^8 \ m/s$

Énergie : $E = h \times \nu$ avec $h = 6,62 \times 10^{-34} \ m^2.kg.s^{-1}$ et $\nu = 5 \times 10^{14}$ .

Ca fait dans les $3 \times 10^{-15}$ Joules c’est-à-dire pas lourd ! 10 milliards de photons chauffent une gouttelette d’eau de un millionième de degré.

Si les photons ne sont pas absorbés, mais simplement réfléchis (par un miroir, etc…) leur énergie $h\nu$ n’est pas absorbée.

La lumière solaire, hors de l’atmosphère et au niveau de la Terre, apporte 1353 Joules par seconde et par mètre carré (1353 Watts par mètre carré) ce qui fait… beaucoup de photons !

Voilà pour l’énergie. Ça chauffe (surtout ce qui est noir, d’où l’intérêt du bronzage ?) mais ça ne pousse pas. Il nous faut autre chose.

Prenez des balles de tennis, et lancez-en une chaque seconde (très fort) sur un mur : le mur s’écroulera (peut-être), à cause de l’impulsion due au choc des balles. Chacune a une quantité de mouvement $P$ où

P = m\cdot v\ (en\ kg\cdot m/s)

$m$ : masse de la balle
$v$ : vitesse de la balle

Si vos balles sont en chewing-gum, le mur reçoit une force $F = P$ (pour $1\ balle/sec$ , en Newton). Si elles rebondissent, la force est doublée puisque le mur doit renvoyer chaque balle après l’avoir arrêtée.

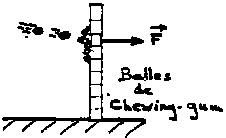
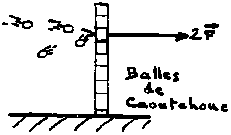
Vous avez compris : les photons n’ont pas de masse, mais leur vitesse est tellement grande qu’on peut leur associer une quantité de mouvement.

Photon : $P = \frac{h\nu}{c} = \frac{E}{c}$

où $c = 299 \ 792 \ 458 \ m.s^{-1}$ (la vitesse de la lumière). Pour la démonstration. il suffit d’écrire $E = m \cdot c ^2$ et vous retrouverez $P = mv$ (ça ne prouve rien mais ça suffira ici !)

Imaginez donc une voile solaire parfaite : une feuille de mylar aluminisé, réfléchissant tout comme un excellent miroir. Si on place 1 mètre carré de ce matériau face au Soleil, on ressentira une poussée du même type que le mur aux balles de caoutchouc :

$Force = \frac{2 \times énergie \ reçue}{c}\\$

$\frac{F}{1 m^2} = \frac{2 \times 1353 W}{3 \times 10^8}\\$

Soit environ $0,903 \ N$

Presque 1 milligramme de force par mètre carré ! Ce n’est déjà pas si mal ; cela ferait 9,2 grammes par hectare.

En fait, c’est presque ça, mais la situation est un peu plus compliquée :

D’abord, aucun matériau n’est parfaitement réflecteur : une partie des photons est absorbée (balles de chewing-gum), i.e. le coefficient de réflectivité r est plutôt 0.9 que 1. La force devient :

$F = \frac{(1+r) \times Énergie}{c}$ , soit environ $0,874 \ mg/m^2$

Parmi ceux qui sont réfléchis, certains le sont dans n’importe quelle direction (surface non spéculaire). Le coefficient s traduisant le taux de spécularité dépend de la propreté du matériau, de son vieillissement etc. ; s vaut environ 0.9 pour une voile neuve (non froissée) (90% des photons réfléchis le sont à angle droit pour une voile perpendiculaire au soleil). Exemple : imaginez que votre mur de tennis soit en tôle ondulée… ceux qui ne sont pas réfléchis spéculairement le sont de manière plus ou moins lambertienne. Une réflexion parfaitement lambertienne (exemple un papier blanc très mat et granuleux) correspond à une répartition hémisphérique des rayons réfléchis ; l’impulsion moyenne communiquée par le photon réfléchi devient la moitié de ce qu’elle serait dans le cas spéculaire (faites l’intégrale, vous verrez) : le coefficient lambertien b est 0,5. Dans la pratique, ce coefficient vaudra entre 0,5 et 0,8.

La force vaut maintenant :

$F = \frac{énergie}{c} \times (1+rs+r(1-s)b)$ avec $r = 0,9, \ s = 0,8$ et $b = 0,7$

Notre mètre carré au soleil reçoit :

F = 0,849 \ mg \ (8,5 \ g/ha)

Ce qui est absorbé est réémis en infrarouge, selon les émissivités et les coefficients lambertiens de chaque face ; si une différence de température existe entre les deux faces, il faut en tenir compte. Dans la cas qui nous intéresse d’une voile aluminisée à deux faces, la réémission infrarouge est symétrique et son effet est nul.

Il faut aussi tenir compte de l’émission infrarouge et de l’albédo de la Terre, qui sont loin d’être négligeables en orbite basse. À 36000 km , l’effet terrestre est de deuxième ordre.

Si la voile n’est pas perpendiculaire au soleil mais s’en écarte d’un angle $a$ , l’énergie reçue est multipliée par $cos(a)$ . Les photons réfléchis de façon spéculaire repartent avec le même angle $a$ par rapport à la normale. On applique un nouveau coefficient $\cos a$ lorsqu’on projette leur action sur l’axe normal. La réflexion lambertienne n’est pas modifiée. La force normale par $m^2$ s’écrit (en l’absence d’effet infrarouge):

FN = \frac{1353 W \cos a ((1+rs) \cos a+rb(1-s))}{c}

Une force tangentielle, généralement négligeable, est due aux photons absorbés ou réémis de façon non spéculaire :

FT = \frac{1353W \cos a \sin a (1-rs)}{c}

Et maintenant, comment utiliser cette force pour naviguer dans l’espace ?

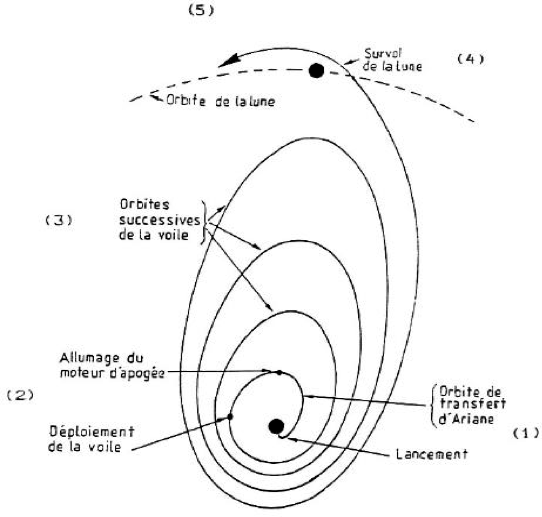
Pour modifier leur orbite, les satellites classiques sont équipés de tuyères qui expulsent à grande vitesse le gaz produit par une réaction chimique. À l’échelle de la durée de vie du satellite, ces manœuvres peuvent être considérées comme instantanées. Leur effet est de transférer le satellite de son orbite initiale à une orbite nouvelle définie par le point où a eu lieu la manœuvre et le vecteur vitesse résultant de la manœuvre.

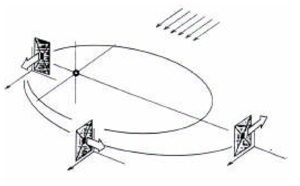
Dans le cas d’une voile solaire, la modification de trajectoire est un processus permanent, dont l’effet sur l’orbite ne peut se mesurer qu’à long terme, en faisant appel à des analyses mathématiques plus complexes. L’élément déterminant pour le contrôle d’orbite d’une voile solaire est l’angle que fait la normale à la voile par rapport à son vecteur vitesse.

Il est intéressant de remarquer que l’accélération gravitationnelle, attractive, et la pression photonique, répulsive, agissent toutes les deux avec une intensité inversement proportionnelle au carré de la distance au Soleil, ce qui induit qu’un dimensionnement quelconque de voile solaire aura des performances identiques où que soit la voile dans le système solaire (tant qu’elle n’est pas à proximité d’un autre corps comme une planète).

Voyons quelques cas simples :

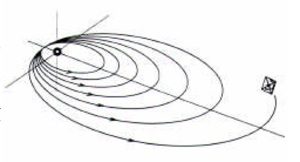
•une orientation de la normale selon le vecteur vitesse mais dirigée dans le sens du mouvement, conduit à une spirale vers l’extérieur.

•au contraire, si la voile est orientée de telle manière que sa normale est alignée avec le vecteur vitesse, orientée en sens inverse du mouvement, la vitesse de la voile est diminuée en permanence. On a donc une configuration de freinage, amenant la voile à se rapprocher du corps attractif selon une spirale.

•un cas particulièrement intéressant est celui de la «lévitation» des orbites.

Si la voile, sur une orbite héliocentrique, est dirigée en permanence vers le Soleil, la poussée photonique se retranche de l’attraction gravitationnelle du Soleil. Tout se passe alors pour la voile comme si le Soleil était plus léger, ce qui permet d’obtenir des orbites d’une période donnée à une distance du Soleil inférieure à la distance correspondant normalement à cette même période.

En résumé :

Une poussée dans le sens de la vitesse fait évoluer en spirale vers l’extérieur
Une poussée contre le sens de la vitesse fait évoluer en spirale vers l’intérieur
Une poussée perpendiculaire à la direction de la vitesse fait évoluer le plan de l’orbite.