1 – La pression photonique
La pression photonique est due à l’échange de quantité de mouvement entre les photons et la surface qu’ils rencontrent, en réflexion, en émission, ou en absorption. Les photons transportent l’énergie :
E = mc2 = hc/l
où c est la vitesse de la lumière, m la masse relativiste, h la constante de Planck (6,626068 × 10-34 m2 kg / s) et l la longueur d’onde.
Ils possèdent une quantité de mouvement :
p = mc = h/l.
Ces équations sont valables pour un photon aussi bien que pour un flux. La quantité de mouvement d’un flux est alors :
p = E/c,
où E est l’énergie du flux.
Si le flux vient du soleil dont l’intensité W est de 1353 W/m2 à la distance R = 1 UA, la pression (force par m2) exercée sur une surface plane totalement absorbante dont la normale fait un angle alpha avec la direction du flux est alors :
p = W/c cos2alpha/R2
soit 4,563 10-6 N/m2 à midi au niveau de la Terre, ou encore 4,476 grammes-force à l’hectare. La force est dirigée le long de la trajectoire du photon, opposée au soleil.
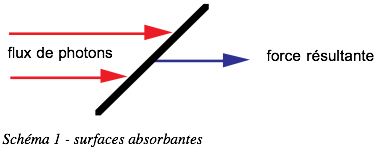
Si la surface est parfaitement réfléchissante, les photons repartent symétriquement à la normale et échangent une fois de plus leur quantité de mouvement, ce qui double la pression.
Nous arrivons dans notre exemple, à une UA, à :
p = 9,126 cos2teta N/m2.
La force résultante est alors dirigée le long de la normale à la surface. Ce point est très important car en orientant la surface, on oriente la force, et il devient possible de naviguer. Les voiles solaires sont donc réfléchissantes pour deux raisons : une force photonique double d’une part, et d’autre part la possibilité de contrôler l’orientation de cette force :
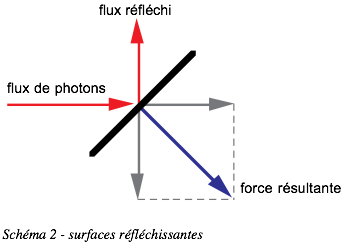
En introduisant la densité surfacique sigma (g/m2) de la voile solaire, on obtient l’accélération :
gamma = 9,126 cos2teta / sigma mm/s2
Par exemple, une voile de 400m2 (20m x 20m) de 100 Kg peut avoir une accélération de 4 10-2 mm/s2, soit 3,5 m/s par jour, soit encore plus de 1 km/s par an.
Les réflecteurs réels ne respectent pas complètement la théorie précédente. Ils absorbent un peu de la lumière incidente, de l’ordre quelques pour cent, et la réémettent principalement dans la longueur d’onde infrarouge de part et d’autre de la surface, avec la force photonique associée. D’autre part, la réflexion n’est pas purement spéculaire mais aussi un peu diffuse. Quelque 10% du flux incident ne suit pas la loi du cos(alpha) et est réémis par diffusion.
Enfin, les défauts de planéité de la surface aux diverses échelles provoquent une dispersion des rayons réfléchis et une imprécision sur la position de la normale à la surface de plusieurs degrés.
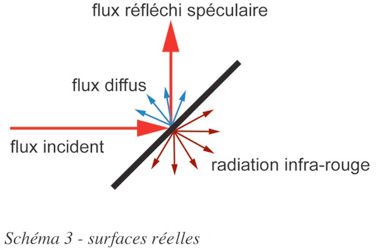
On peut s’attendre à une force photonique réelle 10 à 15% plus faible que le calcul théorique, et à une variation de son orientation de 10 degrés. Ces valeurs dépendent du concept architectural de la voile et de sa réalisation. Des études récentes ont affiné les modèles mais seule une expérimentation en vol les validera.
2 – Caractéristiques de la navigation
La force photonique appliquée à une structure de quelques centaines de m2 est de l’ordre de quelques dizaines de milli-newtons, modulée par le cos(a) de l’angle d’aspect solaire. Cette force est inférieure, mais comparable, à celle produite par un propulseur ionique (les moteurs de la sonde japonaise Hayabusa par exemple, délivraient une poussée de 5 mN).
Bien entendu son grand avantage est qu’elle agit continûment sans consommation de propergol et peut créer des incréments de vitesse considérables.
La force photonique présente quelques caractéristiques propres :
2.1 – Effet en 1/R2
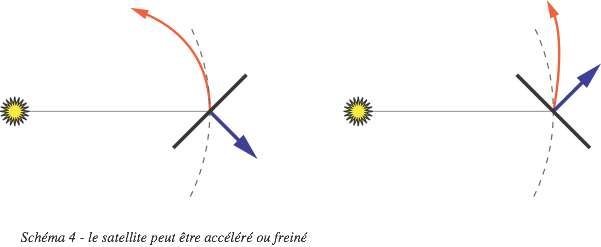
Bien que la force photonique soit toujours dirigée à l’opposé du soleil, il est possible de manœuvrer pour se rapprocher autant que pour s’éloigner du soleil. D’une façon générale, on démontre que quel que soit l’objectif orbital à atteindre, il existe une orientation de la voile qui permet de l’obtenir.
La trajectoire héliocentrique qui se rapproche le plus du soleil est une spirale obtenue pour un angle d’aspect solaire constant de 35,3 °, de même que celle qui s’en éloigne le plus.
2.2 – Accélération et effet sur les orbites
La force photonique solaire est en 1/R2, tout comme l’attraction gravitationnelle. Pour une voile solaire faisant face au soleil, tout se passe comme si la masse du soleil était un peu plus faible. Ceci a pour conséquence la possibilité – envisagée pour certains types de missions, comme Vigiwind – de maintenir une voile sur une orbite de même période que celle de la Terre, mais à une distance moindre du soleil.
Par ailleurs, dans l’idéal, une voile solaire très performante d’accélération caractéristique 5.93 mm/s2, c’est-à-dire égale à l’accélération du champ de gravité du soleil, se déplacerait en ligne droite dans le système solaire. Cette accélération correspond à une masse surfacique de 1,4g/m2.
La rotation du plan de l’orbite est possible avec le même angle, mais, du fait de la loi en 1/R2, la variation angulaire obtenue sur une orbite est constante quel que soit le demi-grand axe de l’orbite. Elle sera donc beaucoup plus rapide pour des orbites proches du soleil de périodes courtes. Cette caractéristique peut être mise à profit pour créer des orbites héliocentriques rétrogrades irréalisables par des moyens classiques. En effet, la vitesse de la Terre étant de l’ordre de 30 km/s, une orbite rétrograde nécessiterait un incrément de vitesse de 60 km/s. La stratégie proposée par le JPL (NASA) pour un rendez-vous avec la comète de Halley – dont l’orbite est rétrograde – était d’utiliser une voile solaire qui spirale vers le soleil, d’effectuer alors le changement de plan et de revenir par la spirale inverse au niveau de la comète
2.3 – Orbite dans l’environnement de la Terre
Pour une voile solaire d’orientation fixe sur une orbite terrestre, l’effet de la pression photonique sur les paramètres d’orbites est en général nul au premier ordre. Un effet éventuellement positif sur une demi-orbite est annulé par celui obtenu lors de la demi-orbite suivante. Pour être efficace, la voile doit être contrôlée dans son attitude avec de larges amplitudes, à la période orbitale, avec des vitesses de rotation d’autant plus rapide que la vitesse angulaire sur l’orbite est grande.
Sur les orbites très basses, la voile solaire multiplie l’effet du frottement atmosphérique par sa grande surface, ce qui peut précipiter le retour sur Terre du satellite.
Sur les orbites basses ou moyennes, au delà de 3 000 km d’altitude, le modèle de force est complexifié en raison des éclipses plus fréquentes et de l’albédo terrestre produisant une force photonique pouvant atteindre 30% de la force solaire maximum (et donc dépasser par endroit celle du soleil pour peu que la voile soit «en drapeau»). Le mouvement d’attitude doit donc être plus rapide.
Sur des orbites plus hautes, la voile solaire peut donner des résultats intéressants pour des mises ou maintient à poste, ou des évolutions d’orbite par exemple dans le système Terre-Lune. Il faudra de l’ordre d’une année pour rejoindre la Lune depuis une orbite géostationnaire avec une voile solaire de masse surfacique 0,25.
